![[PukiWiki] [PukiWiki]](image/ROBO192.png)
![[PukiWiki] [PukiWiki]](image/ROBO192.png)
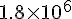 [m] となる。
[m] となる。
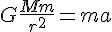 から、
から、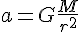
6.8 * 10^-11 * 7.4 * 10^22 / ( 1.8*10^6 )^2;から答えは 1.55 [m/s^2]
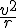 である。これが、1.7[m/s^2] と等しいことから求まる。
である。これが、1.7[m/s^2] と等しいことから求まる。
solve ( v^2/(1.8* 10^6) = 1.55, v ); float(%);答えは 1.67[km/s]
2 * %pi * 1.8 * 10^6 / 1670; float(%);答えは 6800 秒
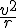 が重力によって得られればそのようになる。
が重力によって得られればそのようになる。
solve( v^2/18=9.8, v); float(%);答えは 13.3 [m/s]
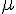 と置くと次式が成り立つ。
と置くと次式が成り立つ。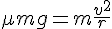
solve( \mu * 9.8 = (0.5)^2/0.3, \mu ); float(%);よって答えは 0.085
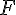 とする。すると、次式が成り立つ。
とする。すると、次式が成り立つ。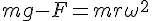
solve( 55 * 9.8 - F = 55 * 20 * ( 2*%pi / 9.0 )^2, F); float(%);答えは 2.87 [N]
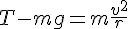
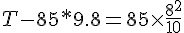
solve( T - 85 * 9.8 = 85 * 64/10 , T);T は 1377 [N] であるので、ロープは切れる。
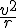 の加速度を持つ。
の加速度を持つ。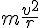 が作用していると考える。
が作用していると考える。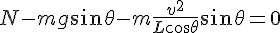
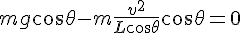
solve( [ N - m*g*sin(theta) - m * v^2/( L * cos(theta) ) * sin(theta)= 0, m * g * cos(theta) - m * v^2 / L = 0], [N, v]);よって、
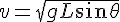
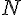 は
は 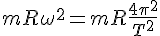 に等しい。
に等しい。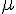 を掛け合わせると、鉛直方向の(最大)摩擦力がわかる。
を掛け合わせると、鉛直方向の(最大)摩擦力がわかる。solve( mu * m* R * (4*%pi^2)/T^2 = m * g, T );よって、
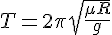
2 * %pi * sqrt( 0.4 * 4 / 9.8 );周期は 2.54 秒, 1分間には、60/2.54 = 23.6 回転
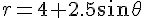
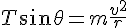
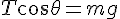
solve( [ r = 4 + 2.5 * sin(theta), T * sin(theta) = m * v^2 / r, T * cos(theta) = m * g], [T, v, r]);
subst( 28/180*%pi, theta, %); subst( 9.8, g, %); float(%);よって、5.19[m/s]
subst( 50, m, %);よって555[N]