![[PukiWiki] [PukiWiki]](image/ROBO192.png)
![[PukiWiki] [PukiWiki]](image/ROBO192.png)
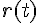 は
はr(t) := 18 * t * i + ( 4 * t - 4.9 * t^2 ) * j;
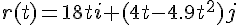
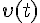 は、上の結果を微分して得られる。
は、上の結果を微分して得られる。v(t) := diff( r(t), t); v(t);
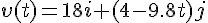
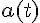 は、上の結果を微分して得られる。
は、上の結果を微分して得られる。a(t) := diff( v(t), t); a(t);
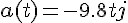
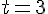 を代入する。
を代入する。r(3);
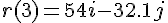
v(3);
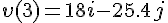
a(3);
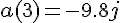
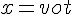 と表される。一方、y方向の位置は y座標
と表される。一方、y方向の位置は y座標 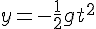 と表される。これらから t を消去する。
と表される。これらから t を消去する。
eliminate( [ x = vo * t, y = -1/2*g*t^2], [t]); solve( %, y);
solve( -0.21 = - 9.8 * ( 3.0 )^2 / 2 / vx^2 , vx ); float(%);答えは 14.5 m/s
solve( 1.90 - 1.00 = 1/2 * 9.8 * t1^2, t1); solve( 1.90 - 0.15 = 1/2 * 9.8 * t2^2, t2); float( 3/7 + sqrt( 5/ 14 ) );~答えは 1.03[s]
float(8.90/1.03);答えは 8.64[m/s]
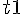 の間に鉛直方向の速度がゼロになったことから求まる。
の間に鉛直方向の速度がゼロになったことから求まる。float( 9.8 * 3/7 );答えは 4.2 [m/s]
float( atan2( 4.2, 8.64) / %pi * 180 );答えは 25.9度
solve( [ 8.90 = vx * t2,
1.90 = 1.00 + vy * t1 - 1/2 * 9.8 * t1^2,
0.15 = 1.00 + vy * t2 - 1/2 * 9.8 * t2^2,
0 = vy - 9.8 * t1],
[vx, vy, t1, t2]);
float(%);
答えは4組でてくる。それぞれ、どのような物理学的な意味があるのか、考えてみよう。solve( [ 50 = 40 * cos( 30/180 * %pi ) * t, y = 40 * sin( 30/180 * %pi ) * t - 1/2 * 9.8 * t^2], [t, y ]); float(%);答え 18.7 m
float( solve(150 = v^2 / 9.8, v ) );打ち出した時の速度は 38.3[m/s] である。これを 20 度で打ち出す。
float( 38.3^2 * sin ( 20 * 2 /180*%pi )/9.8 );答えは 96.2 [m] となる。
solve( [ x = 8 * cos( 20 / 180 * %pi) * 3, y = -8 * sin( 20 / 180 * %pi )*3 - 1/2 * 9.8 * 3^2 ], [ x, y ]); float(%);答え 22.6m
solve( -10 = -8 * sin( 20 / 180 * %pi ) * t - 1/2 * 9.8 * t^2, t );解を吟味して、1.18 s を採用する。
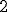 ]
]float( 4^2/20 );答えは 0.80 [m/s
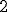 ]
]sqrt( 0.60^2 + 0.80^2 ); float( atan2( 0.80, 0.60) / %pi * 180 );答えは、大きさが 1.0 で、角度は進行方向から 53 度ずれた方向
float( (4.3)^2/0.6 ); float( (6.5)^2/0.6 );
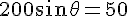 であることに気づく。これを解く。
であることに気づく。これを解く。solve( 200 *sin(theta) = 50, theta); float( % / %pi * 180 );答えは 14.5 度である。
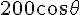 が答えである。
が答えである。
float( 200 * cos( 14.5 / 180 * %pi ));答えは 194[km/h]
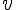 とすると、
とすると、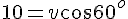 となる。これを解く。
となる。これを解く。solve( 10 = v * cos( 60 /180 * %pi ), v );こうして得られた打ち上げ時の速さ 20 [m/s]から、打ち上げ時の鉛直速度を求める。
v1 : 20 * sin( 60/ 180 * %pi );速度
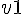 で打ち上げたボールは、時間
で打ち上げたボールは、時間 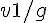 かけて速度がゼロになり、最高点に達する。そこで、最大到達高度は次のようになる。
かけて速度がゼロになり、最高点に達する。そこで、最大到達高度は次のようになる。
1/2 * 9.8 * (v1/9.8)^2;答えは 15.3 [m]
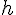 から、速度
から、速度 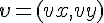 をもって打ち出された物体はどこまで到達するだろうか。
をもって打ち出された物体はどこまで到達するだろうか。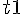 , 最高点から地表まで落下するまでの時間を
, 最高点から地表まで落下するまでの時間を 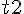 とする。すると、
とする。すると、t1(vy) := vy/g; solve( 1/2 * g * (t2)^2 = 1/2 * g * t1(vy)^2 + h, t2 ); t2(vy,h) := sqrt( vy^2 + 2 * g * h )/g;求める距離
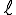 は
は 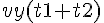 である。
である。l(vx,vy,h) := vx * ( t1(vy) + t2(vy,h) ); l(vx,vy,h);こうして新たな公式
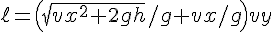 が得られる。
が得られる。l( 1.5 * sin (30/180*%pi), 1.5 * cos (30/180*%pi), 2.1 ); float( subst( 9.8, g, %) );答えは 0.60 [m]
l( 1.5 * sin (30/180*%pi), -1.5 * cos (30/180*%pi), 2.1 ); float( subst( 9.8, g, %) );答えは 0.40 [m]
sqrt( (1.5^2/1.2 * cos(30/180*%pi))^2 + (1.5^2/1.2 * sin(30/180*%pi) + 9.8 )^2 );答えは 10.9 [m/s^2]
100+30*3;190 [m/s] であり、進んだ距離は
1/2 * 30 * 3^2 + 100 * 3;435 [m] である。高度はこれに sin 53°をかけて得られる。
float( 435 * sin (53/180* %pi) );したがってこのときの高度は 347 [m]である。
float( 190 * cos(53/180* %pi) ); float( 190 * sin(53/180* %pi) );から、( 114[m/s], 152[m/s] )となる。最高点に達するまでの時間は、
152/9.8;15.5[s]となる。
t1(vy) := vy/g; t2(vy,h) := sqrt( vy^2 + 2 * g * h )/g;であるから、最初の3 秒と合わせて、
t1(152) + t2( 152,347) + 3; float( subst( 9.8, g, %) );36.2[s] を得る。
435 * cos(53/180*%pi) + 36.2 * 190 * cos(53/180*%pi);答えは、
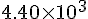 [m]
[m]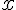 )方向 :
)方向 : 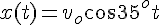
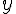 )方向 :
)方向 : 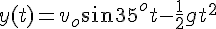
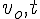 が未知数である。
が未知数である。
solve( [ 130 = vo * cos(35/180*%pi) * t, 20 = vo * sin(35/180*%pi) * t - 1/2 * 9.8 * t^2], [vo, t]); float(%);これらから、
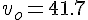 [m/s],
[m/s], 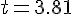 [s]
[s]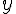 方向の速度だけ変化する。
方向の速度だけ変化する。
atan2( 41.7 * sin(35/180*%pi) - 9.8 * 3.81, 41.7 * cos(35/180*%pi));答えは -21.4 [m/s]
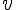 とする。また、屋根で滑っていた時間を
とする。また、屋根で滑っていた時間を 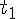 空中に浮いていた時間を
空中に浮いていた時間を 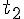 とする。すると、これらの量について、次の式が成り立つ。
とする。すると、これらの量について、次の式が成り立つ。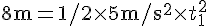
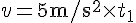
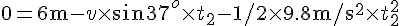
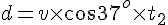
solve( [8 = 1/2 * 5 * t1^2, v = 5 * t1, 0 = 6 -v * sin(37/180*%pi) * t2 - 1/2 * 9.8 * t2^2, d = v * cos(37/180*%pi) * t2], [t1, t2, d, v]); float(%);以上から $ t_1 = 1.79[s], t_2 = 0.69[s], v = 8.94[m/s], d = 4.90[m]$
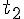 を用いると、求める速さは次のようになる。
を用いると、求める速さは次のようになる。
sqrt( (8.94 * sin(37/180*%pi) + 9.8 * 0.686)^2 + (8.94 * cos(37/180*%pi))^2); float(%);答え 14.1 m/s
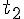 から 0.69[s]
から 0.69[s]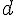 から 4.90[m]
から 4.90[m]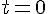 とする。鷹の降下する速度を
とする。鷹の降下する速度を 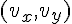 とし、鷹が再び鼠をとらえた時刻を
とし、鷹が再び鼠をとらえた時刻を 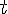 とする。すると、次のような式が成り立つ。
とする。すると、次のような式が成り立つ。![v_y (t-2[{\rm s}]) = \frac{1}{2}g t^2 = 197 [{\rm m}]](cache/f783bb0bf736b0e31793f75feb7c9231.mimetex.gif)
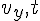 が求められる。
が求められる。
solve( [197 = 1/2 * 9.8 * t^2, vy * (t-2) = 197 ], [t,vy]);
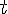 = 6.34[s],
= 6.34[s], 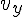 = 45.4 [m/s]
= 45.4 [m/s]![v_x (t-2[{\rm s]]) + (2 * 10.0) [{\rm m}] = (10.0 * 6.34) [m]](cache/af748cf23946bd103013aeb6d5469a2a.mimetex.gif) これから次のように
これから次のように 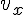 が求められる。
が求められる。
solve( vx * (6.34-2) + 2 * 10.0 = 10.0 * 6.34, vx );よって、
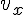 = 10.0 [m/s]
= 10.0 [m/s]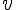 とすると、
とすると、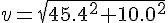 = 46.5[m/s]
= 46.5[m/s]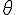 とすると、
とすると、
atan2( 45.4, 10.0 );
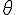 = 77.6°
= 77.6°