波の共鳴 †
GeoGebra なら数式をそのまま絵にできるので、波の共鳴を表すアニメーション作成も容易です。
- 図の見方
- 赤い線 : 右へ進む波。この波は何らかの波源によって生成されているとします。
- 緑色の線 : 赤い線で表される波が、右端で反射したときの反射波。境界条件は、自由端か固定端か選べます。
- 黒い線 : 上記二つの波を足し合わせたもの。
- 黄色の線 : 緑色の線で表される波が、左端で反射したときの波。境界条件は、自由端か固定端か選べます。非表示にもできます。
- 波の速度 : 1 で固定してあります。
- 初期設定のアニメーション
画面左下のマークをクリックしてアニメーションを開始します。この状態は共鳴が生じている状態です。
次のように、順番に観察して下さい。
- 入射波(赤い線, 外部からエネルギーが注入された波とします。)は右に進みます。
- 右端は自由端になっているので、反射波(緑色の線)は、入射波と同じ値になります。
- また、反射波は、同じ振動数と同じ波長の波として、左に進みます。
- 左端を観察すると(たまたま)入射波と反射波は、値が逆転しています。つまり、合計はゼロです。
このような時、固定端反射の境界条件が満たされるので、反射波(緑色の線)の反射波が、再び、入射波(赤い線)と一致します。
こうして、パイプの中は位相が揃った波で満たされることになり、互いに打ち消すことがなくなります。
そして、外部から注入されたエネルギーがたまりつづけます。
- 遊び方
![[PukiWiki] [PukiWiki]](image/ROBO192.png)
![[PukiWiki] [PukiWiki]](image/ROBO192.png)
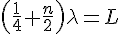 で共鳴が起こるので、その値にしてみる。
で共鳴が起こるので、その値にしてみる。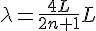 なので、
なので、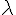 = 20, 6.67, 4, 2.86, …
= 20, 6.67, 4, 2.86, …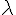 の値の時に限って、黄色の波が赤い波と一致することを確かめる。
の値の時に限って、黄色の波が赤い波と一致することを確かめる。