![[PukiWiki] [PukiWiki]](image/ROBO192.png)
![[PukiWiki] [PukiWiki]](image/ROBO192.png)
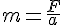 ただし、
ただし、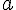 は加速度。
は加速度。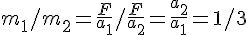
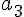 とすると、
とすると、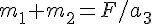 , ここで、
, ここで、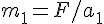 ,
, 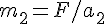 を代入すれば、
を代入すれば、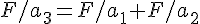 , よって
, よって 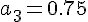 m/s
m/s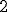
sqrt( 20^2 + 15^2 )/5;より 5 m/s/s。
float( atan2( 15,20) / %pi * 180 );より、F1 の向きから F2 の向きへ 36.9 °
float(sqrt( (20+15*cos(60/180*%pi))^2 + (15*sin(60/180*%pi))^2 )/5); float( atan2(15*sin(60/180*%pi), 20+15*cos(60/180*%pi)) / %pi * 180 );から、大きさ 6.08, 向き 25.3 °
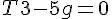
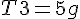
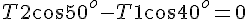
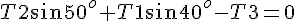
solve( [ T2 * cos(50/180*%pi) - T1 * cos(40/180*%pi) = 0, T2 *sin(50/180*%pi) + T1 * sin(40/180*%pi) - 5*9.8 = 0], [T1, T2]); float(%);答えは、T1=31.5[N], T2=37.5[N]
solve( [T1*cos(60/180*%pi) - T2 = 0, T1*sin(60/180*%pi) - T3=0, T3-10*9.8=0],[T1,T2,T3]); float(%);答えは T1=113[N], T2=56.6[N], T3=98.0[N] (本当は2桁)
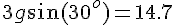
 とする。
とする。
solve( [ 55 * t - 1/2 * a * t^2=1000, 55 - a * t = 0 ], [a, t]); 1.51 * 8820/9.8 ;答えは 1.36 ×
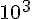
solve( 400^2 = 0^2 + 2 * a * (0.15 - 0), a); float(%);a は 533333[m/s^2] となる。
これに弾丸の質量をかければよい。 % * 0.012;答えは
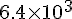 [N]
[N]atan2(390, 180) / %pi *180; float(%);から、東から北に
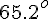 ずれた方向である。
ずれた方向である。sqrt( 180^2 + 390^2 ); float(%);から 430 [N] であり、これを質量で割れば加速度が出る。
%/270;答えは 1.59 [m/s^2]
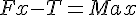
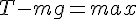
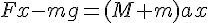 となる。ax が正である条件は、
となる。ax が正である条件は、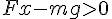 であるので、答えは
であるので、答えは
2*9.8;19.6[N]
 である。これを3つめの式に代入すると、
である。これを3つめの式に代入すると、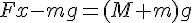 となり、これを Fx について解くと、
となり、これを Fx について解くと、solve( Fx - m*g= -(M+m)*g, Fx ); subst( 9.8, g, %); subst( 8, M, %); subst( 2, m, %);答えは -78.4[N]
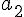 に対して
に対して 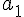 は2倍の値になっていることに気を付ける。
は2倍の値になっていることに気を付ける。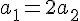
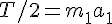
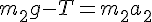
solve( [T/2=m1*a1, m2*g-T=m2*a2, a1=2 * a2], [a1, a2, T]);
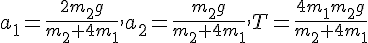
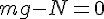
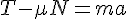
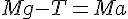
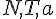 に対して、式が三本だから解ける。
に対して、式が三本だから解ける。solve( [ m * g - N = 0, T - mu * N = m * a, M * g - T = M * a ], [N, T, a] );これから、
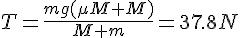
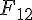 等と表す。すると、運動方程式は、
等と表す。すると、運動方程式は、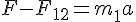
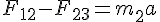
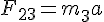
solve( [ F - F12 = m1 * a, F12 - F23 = m2 * a, F23 = m3 * a], [F12, F23, a]);
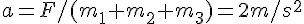
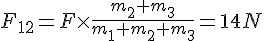
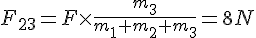
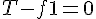
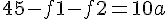
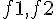 は次のように求められる。
は次のように求められる。
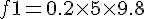
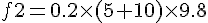
solve( [ 45 - f1 - f2 = 10*a, f1= 0.2 * 5 * 9.8, f2=0.2*15*9.8], [f1, f2, a]);f1=9.8[N], f2=29.4[N], f3=0.58[m/s^2]
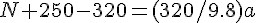
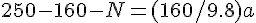
solve( [N + 250 -320=(320/9.8) * a, 250-160-N = (160/9.8) * a], [N, a]);N=83.3[N], a=0.41[m/s^2]