設問 (ベクトルの演算) †
問1 †
ベクトルの演算についていえることは何か。
ベクトルの演算は足し算・引き算・かけ算・割り算が定義されている。
ベクトルとスカラーの間ではいかなる演算もできない。
ベクトルの演算などありえない。
ベクトルの足し算・引き算は、各ベクトルの対応する成分について演算すれば良い。
ベクトルのかけ算・割り算は、各ベクトルの対応する成分について演算すれば良い。
問2 †
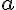 = ( 1, 2, 3 ),
= ( 1, 2, 3 ), 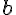 = ( 3, 4, 5 ) の時、
= ( 3, 4, 5 ) の時、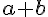 はどのようなベクトルになるか。
はどのようなベクトルになるか。
( 6, 12 )
( 3, 3 )
( 4, 6, 8 )
( 4, 5, 6)
( 5, 6 )
問3 †
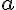 = ( 1, 2, 3 ),
= ( 1, 2, 3 ), 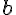 = ( 3, 4, 5 ) の時、
= ( 3, 4, 5 ) の時、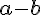 はどのようなベクトルになるか。
はどのようなベクトルになるか。
( 3, 3 )
( 0, 2 )
( -2, -2 )
( 2, 2, 2 )
( -2, -2, -2)
問4 †
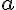 = ( 1, 2, 3 ),
= ( 1, 2, 3 ), 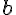 = ( 3, 4, 5 ) の時、
= ( 3, 4, 5 ) の時、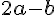 はどのようなベクトルになるか。
はどのようなベクトルになるか。
(0, 2)
(3, 3)
(12, - 12)
(-1, 0, 1 )
( 1, 0,-1 )
問5 †
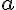 = ( 1, 2, 3 ),
= ( 1, 2, 3 ), 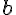 = ( 3, 4, 5 ) の時、
= ( 3, 4, 5 ) の時、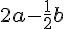 はどのようなベクトルになるか。
はどのようなベクトルになるか。
(0.5, 2, 3.5 )
(-3.5, -2, -0.5 )
( 12, -6)
( 0.5, 0.5 )
(-4, 3 )
問6 †
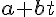 を考える。これが表すものは何か?ただし、
を考える。これが表すものは何か?ただし、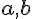 の始点は原点に置かれているとする。また、
の始点は原点に置かれているとする。また、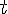 はスカラーで、
はスカラーで、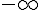 から
から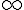 まで変化する量であるとする。
まで変化する量であるとする。
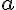
と
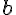
とが作る平行四辺形の内部
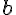
との差が
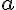
となるようなベクトルの全体
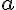
との差が
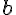
となるようなベクトルの全体
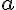
の終点を通り、
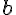
に平行な直線
原点と
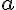
,
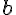
の終点が作る三角形の内部
問7 †
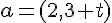 ,
, 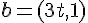 を考える。
を考える。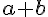 が表すものは何か。ただし、
が表すものは何か。ただし、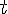 はスカラーで、
はスカラーで、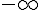 から
から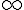 まで変化する量であるとする。
まで変化する量であるとする。
ベクトル
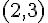
と
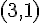
とが作る平行四辺形の内部
ベクトル
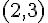
との差が
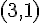
となるようなベクトルの全体
ベクトル
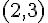
との差が
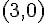
となるようなベクトルの全体
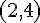
を通り、
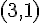
に平行な直線
原点と
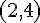
,
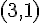
の終点が作る三角形の内部
問8 †
ある座標系から見て、点 A の位置ベクトルが 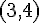 で表されていたとする。座標軸を平行にずらし、点
で表されていたとする。座標軸を平行にずらし、点 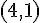 を新たな原点としたとする。新しい座標での点 A の位置ベクトルはどのように表されるか。
を新たな原点としたとする。新しい座標での点 A の位置ベクトルはどのように表されるか。
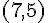
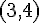
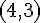
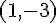
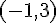
問9 †
ある座標系から見て、点 A の位置ベクトルが 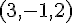 で表されていたとする。座標軸を平行にずらし、点
で表されていたとする。座標軸を平行にずらし、点 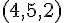 を新たな原点としたとする。新しい座標での点 A の位置ベクトルはどのように表されるか。
を新たな原点としたとする。新しい座標での点 A の位置ベクトルはどのように表されるか。
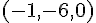
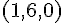
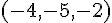
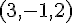
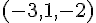
問10 †
ある座標系から見て、点A は静止していたとする。これの座標系に対して速度 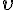 で等速直線運動している座標系から見ると、点 A はどのように運動して見えるか。
で等速直線運動している座標系から見ると、点 A はどのように運動して見えるか。
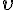
で等速直線運動しているように見える。
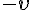
で等速直線運動しているように見える。
最初は静止しているが、次第に速く運動するように見え、最終的に速度
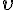
で運動するように見える。
最初は静止しているが、次第に回転するように見え、最終的に等速円運動するようになる。
静止してみえる。
氏名:
![[PukiWiki] [PukiWiki]](image/ROBO192.png)
![[PukiWiki] [PukiWiki]](image/ROBO192.png)